
Connecting scientific equations with reality has long been sought after to generate more effective lab results.
A research team led by Dr. Gregory Reeves is working to speed up the process of taking generalized models or equations and making them match the real world.
Reeves, an associate professor in the Artie McFerrin Department of Chemical Engineering at Texas A&M University, studies the chemical reactions occurring inside cells. By combining more classical mathematical models with optimization techniques, Reeves can better comprehend the cells and have a good predictive model of what's happening inside the cell.
“If we can't understand these reactions well enough to write down equations and make those equations predictive about what could happen next, then we won't be able to do things like control what's happening in the cell,” Reeves said. “As a system, we look at a complicated set of chemical reactions that are taking place inside a biological cell. It becomes imperative to ensure that models are good descriptions of reality. We do that by using optimization procedures.”
In a recently published Oxford Press article, Reeves and two graduate students, Prasad Bandodkar and Razeen Shaikh, combined the power of evolutionary algorithms with classical search methods, such as gradient descent and Newton’s method, to efficiently optimize models to data sets.
“Evolutionary optimization takes its ideas from the scientific theory of evolution, where you start with a whole bunch of random individuals and the ones that are closest to the data make it to the next generation,” Reeves said. “Evolutionary optimization has no intelligence behind it because there's no planning or forward thinking behind it. What we wanted to do with our method is to take the best parts of evolutionary optimization and try to make it faster by putting some intelligence into it.”
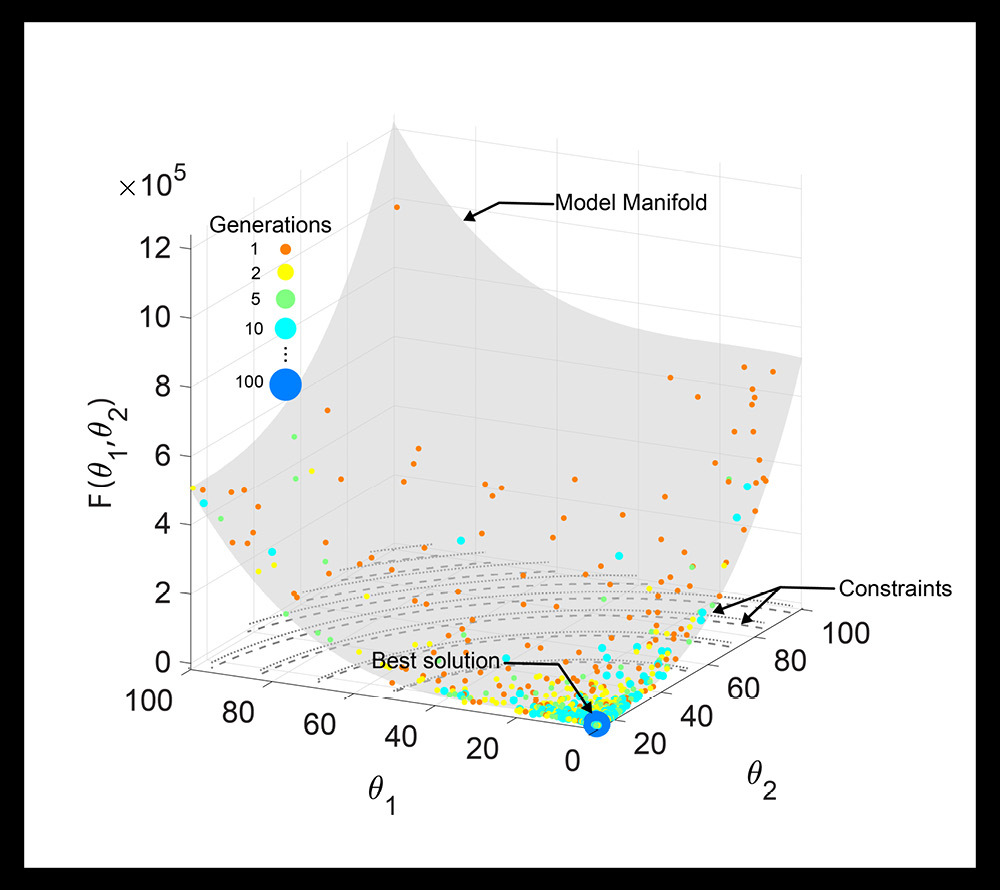
Evolutionary algorithms estimate model parameters, such as “fittest individuals,” by generating a large population of individuals using strategies like recombination and mutation over multiple “generations,” according to the article.
However, like evolution, there is no planning for these algorithms. They examine the fittest individuals in isolation or, at best, combine information between only two individuals. As such, they fail to account for long-range connections that may exist among dozens of the fittest individuals.
“By itself, the evolutionary algorithm simply looks at an individual and decides if it’s relatively fit (close to the data),” Reeves said. “By including gradient descent and Newton’s method to the evolutionary algorithm, the new combined algorithm also looks at the trend of multiple individuals at once to determine the best direction to go in the next step."
Reeves believes this new algorithm could impact a wide range of different approaches to different fields to speed data up and make it more efficient.
All scientific advances are based on a foundation of being able to make observations about the outside world and make generalizations, such as Galileo and the Leaning Tower of Pisa legend and Newton’s acceleration experiment, Reeves said.
“Being able to take these observations about the real world and generalize them into equation format so that you can use the equation to predict what's going to happen next is a major driver to scientific discovery,” Reeves said.